In these processes, fluid turbulence is a key factor. However it is difficult to measure the transient, two-phase flow inherent to wave breaking, despite measurements made with PIV (Particle Image Velocimetry) and LDF (Lasor Doppler Velocimetry) techniques outside the spatial region of air entrainment; a method that allows both high spatial and temporal resolution of flow dynamics inside the breaking wave crest.
Recent studies have demonstrated the use of bioluminescent dinoflagellates to visualize flow fields within Couette and turbulent pipe flow, the visualization of flow separation on a gliding dolphin, and the laminar to turbulent transition on a sphere. Because bioluminescent dinoflagellate flashes in response, they can be used either as markers to illuminate fluid streak lines in complex flows (PIV) or, as we are proposing here, as quantitative indicators of supra-threshold flow agitation. The successful application of this approach to breaking wave dynamics will provide time-evolving estimates of fluid shear stress inside a breaking wave crest on O(ms) time scales and O(mm) length scales.
The IMT Laboratory has conducted experiments measuring the heterogeneous, time-varying shear stress inside a breaking wave using bioluminescent dinoflagellates (pyrocystis fusiformis) as numerous and tiny biological sensors responsive to fluid shear stress.[/vc_column_text][/vc_column][/vc_row][vc_row css=”.vc_custom_1556672727982{padding-right: 25px !important;padding-left: 25px !important;}”][vc_column][vc_custom_heading text=”Breaking Wave Study with Bioluminescence” font_container=”tag:h3|text_align:left” google_fonts=”font_family:Roboto%3A100%2C100italic%2C300%2C300italic%2Cregular%2Citalic%2C500%2C500italic%2C700%2C700italic%2C900%2C900italic|font_style:500%20bold%20regular%3A500%3Anormal”][vc_video link=”https://youtu.be/nujbO76HsN0″ align=”center”][/vc_column][/vc_row][vc_row css=”.vc_custom_1556672808775{padding-right: 25px !important;padding-left: 25px !important;}”][vc_column][vc_custom_heading text=”Experiment” font_container=”tag:h3|text_align:left” google_fonts=”font_family:Roboto%3A100%2C100italic%2C300%2C300italic%2Cregular%2Citalic%2C500%2C500italic%2C700%2C700italic%2C900%2C900italic|font_style:500%20bold%20regular%3A500%3Anormal”][vc_tta_accordion color=”white” c_icon=”chevron” active_section=”0″ collapsible_all=”true” el_class=”accordion”][vc_tta_section title=”Bioluminescent Cell Flashing Models” tab_id=”1550461312534-b12fd594-9c6a”][vc_column_text][6] The use of dinoflagellate cells as quantitative flow indicators requires a model for bioluminescent cell flashing behavior. The model used here is statistical and is based on the fundamental assumption that in some small time interval δt there is a probability p0 that a cell fires, which is equal to

where λ is a parameter that is an intrinsic property of the cell that depends up the reaction of the cell to the local environmental conditions. The cell response that we are primarily concerned with here is the increased probability of flashing that accompanies increasing fluid shear stress. Because the probability of a cell firing increases with increasing λ we shall refer to it as the cell anxiety parameter. The relationship between λ and fluid shear stress is discussed later (see equation (18)). We know from our analysis of prior studies [Latz et al., 1994; Latz and Rohr, 1999; Rohr et al., 1997, 1998, 2002] that the anxiety parameter is a function of the local shear stress, and may also vary with the shear temporal derivative [Blaser et al., 2002]. Thus, by “small time interval” we mean the shear stress and shear derivative can be considered constant within this interval. To calculate the probability that a cell fires within a time interval t over which the shear stress does vary, we divide it into a large number of M consecutive subintervals. Whether or not the cell fires in a subinterval is specified with a Bernoulli variable f, which equals 0 if the cell fires and 1 otherwise. Whether or not the cell fires in a time interval t can be thought of as a sequence of M Bernoulli trials, each one of which occurs during a subinterval Δt = t/M. From our underlying assumption, the probability that an unfired cell fires in the jth subinterval is p0 = λj Δt, where λj is a function of the local shear stress τj during the subinterval. The probability that the cell does not fire is p1 = 1 – p0 = (1 – λj Δt). The probability of a cell surviving the entire interval without firing is the conditional probability that it does not fire in any of the subintervals:
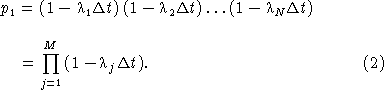
We derive the exponential approximation for this function as follows. To first order in Δt, exp(– λj Δt) ≈ (1 – λj Δt) and
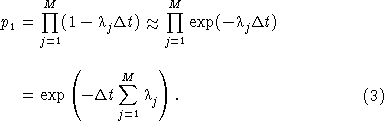
Since M = t/Δt,

and, in the limit as Δt → 0,
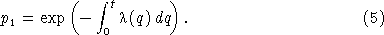
This result states that the probability that a single cell survives a period of variable shear stress without firing is given by a decaying exponential controlled by the integral of the shear stress over time. For the case of time‐invariant stress, the integral in equation (5) simplifies, and we obtain

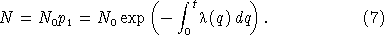
For the case of constant shear stress, equation (7) simplifies to

leading to the expectation that the number of unfired cells in a population subject to constant shear stress will decrease exponentially with time with a decay rate equal in magnitude to the cell anxiety parameter, λ. This prediction is consistent with previous observations [Latz et al., 1994]. They observed that the light output from a population of dinoflagellates subjected to a constant shear stress decays exponentially with increasing time:

where K0 is the photons s−1 per cell at time t = 0, and R is a constant (the decay rate) that depends on species. The number of cells flashing per unit time is equal to −dN/dt, and from equation (8) we have that
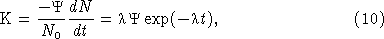
where Ψ is the number of photons emitted per cell. Comparing equations (8) and (9) it is apparent that

[8] In order to estimate shear stress within a breaking wave crest, we need to calibrate images of flashing cells within the wave crest. The first step in this process is to relate the pixel intensity in the images to the number of cells flashing. The light intensity within the images is a measure of the number of photons Γ emitted from a sample volume during a specified integration time Ω. The photon count depends on the number of cells firing in and moving through the imaged sample volume, any absorption and scattering that occurs along the optical path length between the sample volume and the camera, and the solid angle subtended by the camera. The scattering, absorption and solid angle subtended by the camera can be incorporated into a single system‐dependent constant η. The number of photons emitted by a single cell that are gathered by a detector (possibly spread over multiple pixels) is then given by

where we have used the subscript 0 to indicate photons from a single cell, and an over bar to indicate detected photons.
[9] A surrogate for the measured photon count given by equation (12) can be estimated from an image by summing the pixel values along a cell light streak, provided that σ is longer than the cell firing time. Although the track and brightness of the streak depend on the velocity of the firing cell and its locus through the sampling volume, the integrated detector output along the cell path depends only on the total number of photons emitted by the cell and detected by the camera. Thus we have

where zij is the intensity value of the pixel located at position (i, j) within the cell path in the image and the summation is along the entire path. An estimate of the total number of cells firing within a selected region of the image is then:
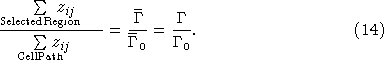
Equation (14) assumes light scattering within a sample volume remains constant between calibration cell region and the measurement region. In fact, the presence of air in the wave crest will change the scattering coefficient. There are two effects that need to be accounted for: the absorption of photons by bubbles along the optical path and the scattering of photons by bubbles to the side and behind. These effects are discussed in greater detail later but for the present we will neglect them as significant sources of bias.
[10] The next step is to relate the number of firing cells to the local fluid shear stress, and we do this by determining the functional dependence between cell anxiety and fluid shear stress. Because the measured decay rate of light emission from populations of cells subject to constant shear stress varies between genera and species, the parameter λ must also depend on dinoflagellate type. At the present time, the sensitivity of the dinoflagellate species used in the experiments (Pyrocystis) to rate of change of shear stress is unknown, and we have made the additional simplifying assumption that λ for Pyrocystis is a function only of the local shear stress, τ:

where α and τ0 are constants which depend on dinoflagellate type. The constant τ0 is needed to account for the observation that cells do not flash until the fluid shear stress has exceeded a critical threshold.
[11] Inherent in this model is that cells have no memory, sensitivity to rate of change of shear stress, and that cells fire only once on the timescales of interest. Although future research may show that cell memory, rate of change of shear stress and multiple cell firing plays a role in cell light emission, we have adopted equation (15) as the simplest canonical model available consistent with observed cell behavior.
[12] We can form an estimate for λ by noting that over the image light integration time, Ω, the total number of cells expected to fire is equal to
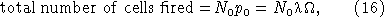
provided that the total number of unfired cells N0 is approximately constant over the integration time (cf. equation (1)). Solving equation (16) for λ and using equation (14) to eliminate the total number of cells fired yields:
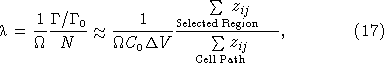
where we have made the approximation that the number of unfired cells is equal to the concentration measured at the start of the experiment multiplied by the sample volume of seawater imaged by a camera pixel. Equation (17) shows that we can make quantitative estimates of λ without having to know the details of the detector geometry and efficiency, provided images with single cell tracks are made for calibration. A first‐order estimate for C0 can be made by manual cell counts before the start of the experiment. A straightforward iterative scheme can be used to reestimate C0 from its initial value and successive estimates of the number of cells fired if the cell firing rate is sufficiently high that the concentration of unfired cells changes by a significant fraction over the experiment time, but this was not necessary for our data.
[13] The process of estimating λ from the images and then the subsequent inversion of λ for τ as described above forms the basis for quantitative estimates of shear stress, which we will refer to as Bioluminescence Imaging.[/vc_column_text][/vc_tta_section][vc_tta_section title=”Application to Laboratory Wave Breaking” tab_id=”1550619966176-7306444f-3b73″][vc_column_text][14] One of our principal motivations for developing the bioluminescence imaging technique is to study fluid shear and energy dissipation within breaking waves. To that end, we present here some preliminary results showing estimates of fluid shear stress and turbulent energy dissipation for a single event. The intention is not to present a definitive study on wave breaking mechanics, but to illustrate the viability of the technique and show that the data obtained falls within the range of values that are expected from prior studies.
[15] A series of experiments were conducted in the Scripps Institution of Oceanography seawater wave flume (33 m long, 0.5 m wide, 0.6 m water depth). Wave packets were generated at one end of the flume using a computer controlled wave paddle which produced plunging breakers approximately 10 cm in height (Figure 1). The amplitude and phase of the wave packet frequency components were generated so that they added constructively to produce a wave that broke consistently at one location [Longuet‐Higgins, 1974]. The wave packet center frequency, wavelength, relative bandwidth, and slope were 0.73 Hz, 2.3 m, 1 and 0.4, respectively. Surface elevation time series computed from pressure measurements made upstream and downstream of the breaking region were used to compute the wave packet energy lost because of breaking and ensure that events were repeatable.
[16] The flume working section was seeded with approximately 0.5 cells mL−1 of P. fusiformis and the density of cells in the test section was checked after breaking events by pump sampling through a calibrated flow agitator (a device similar to a bathyphotometer that quantifies the number of photons emitted by bioluminescent organisms in a known volume [Widder et al., 1993]). The bioluminescence occurring during breaking was imaged at 30 frames s−1 with a video camera and image intensifier mounted on a motion‐controlled sled allowing a single region of the breaking crest to be followed throughout its evolution.
[17] The video images from the test experiment were analyzed using the model described above. To begin, the background noise level was estimated from a dark region of the images and subtracted. Then 5 video frames were averaged to match the camera light integration time with the flash duration of P. fusiformis, which is approximately 0.1 s. The cell path intensity appearing in equation (13)was estimated from the average sum of pixel values along ten selected cell tracks (i.e., Figure 1b). The anxiety parameter (λ for the pixel) was then calculated using equation (17) with Ω = 0.17 s (the image integration time) and ΔVC0 = 0.028 cells per pixel volume (estimated from manual cell counts of pump samples and the pixel sample volume).
[18] This analysis produces a spatial map of λ on pixel length scales. Although the images appear to contain information on these short scales (Figure 2b), the advection of flashing cells across the camera field of view places a fundamental limitation on the spatial resolution of the mapping. P. fusiformis has a bright and long‐lasting “first” flash characteristics (up to 170 ms,) compared with other species, making it easy to image with an intensified video camera [Widder and Case, 1981], but is not an optimal choice for the measurement of stress on short temporal and spatial scales. To obtain a map of λ on the spatial scales determined by cell advection required running the high‐resolution image through a 2 dimensional spatial filter. We used a two dimensional Hanning window with a pixel width characteristic of a typical cell track length (75 pixels). The remaining step was to then relate the filtered estimates for λ to shear stress. From the published decay rates [Latz et al., 1994; Rohr et al., 1997, 2002] for different constant stress levels for various dinoflagellates, including the genera Pyrocystisfrom which we can estimate λ (see equation (15)). From their Table 2 [Latz et al., 1994], we estimate that

for Pyrocystis. Equation (18) has been used to map our measured values of λ to estimates of τ and the resulting images are shown in Figure 2c. The measured shear stress ranges from about 0.2 to 1.0 Pa with peak values of 2.5 Pa. To put these shear stress levels into an oceanographic context, we note that shear stress of the order of 0.1–1.0 Pa has been measured in wave‐forced bottom shears in the surf zone [Rohr et al., 1997], and shear stress in the shallow 2 mm surface layer due to wind forcing is about 0.1 Pa [Cox et al., 1996]. Regions of high shear stress can be seen associated with the collapse of the overturning wave jet (top) and the turbulent eddy formed in the secondary splash‐up in front of the wave crest (middle), which are consistent with expected high‐stress regions imaged using traditional optics [Deane and Stokes, 1998, 2002].
[19] Estimates of turbulent energy dissipation can be obtained by relating the measured shear stress to the turbulent dissipation rate [Latz et al., 1994; Rohr et al., 1997; Garrett et al., 2000]:

[20] Figure 3 shows spatial maps of the turbulent energy dissipation rate during a breaking event, calculated from the inferred fluid shear stress using equation (19)and setting k = 1.
[21] The sequence of images shows the temporal and spatial evolution of the turbulent dissipation through the wave breaking event. By comparing the dissipation maps with the optical images in Figure 2, it is evident that the regions of highest dissipation correspond to cavity crushing and the region of jet/wave face interaction. In addition, the dissipation rate peaks (to about 20 W kg−1 within the intruding jet region on the right side of the middle plate in Figure 3) during the period of most intense sound generation, which is associated with the formation of bubbles [Deane and Stokes, 2002].
[22] It is necessary to create a context for these estimates of spatially and time varying dissipation before comparing them with previous work. Prior estimates of energy dissipation in wave crests do not include temporal and spatial information; they consist of fractional dissipation measured as the ratio of the surface displacement variance downstream and upstream of the breaking events [i.e., Lamarre and Melville, 1991; Loewen and Melville, 1991; Melville, 1994], and dissipation inferred from bubble size distribution measurements [Deane and Stokes, 2002]. It is not possible to make a direct comparison with the results of Melville and coworkers because their measurements of the fractional dissipation are an average over the entire breaking event, which potentially includes multiple plume injections occurring at the beginning and end of the event. We can however, compare our data with that obtained by Deane and Stokes [2002], which represents an estimate of the turbulent dissipation rate within a primary plume injection during the air entrainment phase. This corresponds to the spatially averaged dissipation rate within the crushing cavity and overturning jet and lasts for about 200 ms for these laboratory waves. The average dissipation rate inferred from the scale of the smallest bubble subject to turbulent fragmentation (the Hinze scale), is reported to be 12 W kg−1. For comparison, the average value of dissipation in a box centered on the crushing cavity (Figure 3) is 7.1 W kg−1.[/vc_column_text][/vc_tta_section][vc_tta_section title=”Light Scattering and Absorption by Bubbles” tab_id=”1550620051737-bbe8412b-36eb”][vc_column_text][23] One of the main sources of bias in the images collected using this visualization technique to measure shear stress within wave crests is the scattering and absorption of photons by the bubbles entrained by breaking. A plate illustrating the effects of scattering is shown in Figure 4. The figure is plotted in false color to emphasize light level contours. The white and blue elongated regions correspond to the tracks of light produced by flashing dinoflagellates as they moved past the camera. The red granular regions surrounding the plankton tracks are the result of light scattered from microbubbles in the wave crest. These low levels of light do not occur in regions where microbubbles are absent. For example, the tracks in the box “A” (Figure 4) are behind the actively breaking wave crest in a region with few bubbles [Deane and Stokes, 2002], and do not exhibit low‐light granularity.
[24] The effects of scattering are removed by subtracting the mean scattering intensity from the images (thresholding). This is a subjective procedure: the intensity level used here was determined by examining a number of images and selecting a level that removed most of the granular region. This same threshold level was applied to all images including those used to calibrate the cell emission intensity. The result of thresholding is shown in the right hand plate in Figure 4.
[25] The effects of light absorption by bubbles depends on the transmission path length through the bubbly mixture. An opaque divider was added to the wave flume specifically to limit the length of the transmission path and minimize the effects of absorption by bubble occlusion (see Figure 1a).
[26] These measures combined with the reasonable agreement between quantitative analysis of shear stress levels and those expected to exist on the basis of the work of ourselves and others, albeit for a limited data set, helps justify our treatment of scattering and absorption. A more rigorous evaluation of bubble effects could be made by imaging a calibrated light source inside a breaking wave crest and this will be done in future experiments.[/vc_column_text][/vc_tta_section][vc_tta_section title=”Concluding Remarks” tab_id=”1550620100385-3a82d488-2401″][vc_column_text][27] The formulation of a statistical model of dinoflagellate cell firing behavior and the development of a calibration technique (bioluminescence imaging) has allowed us to produce quantitative images of the evolving fluid shear stress field within breaking wave crests. The images show high rates of turbulent energy dissipation in the jet/wave face interaction region consistent with earlier optical observations.
[28] The technique is based on two parts: a statistical model for single cell flashing behavior and its relationship to fluid shear, and a calibration methodology for analyzing images. The fundamental assumption in the statistical model is expressed by equation (1), which states that over some small time interval, the probability that a cell flashes is proportional to time. An additional assumption is that cells produce a detectable flash only once (a good assumption for some, but not for all species). When applied to populations of cells, the statistical model produces results consistent with available biological data for the special case of constant shear stress; the case of time‐varying shear remains to be examined. Cells flash in response to many kinds of stimulation; the focus here is on stimulation induced by fluid shear. The model we have adopted relating the anxiety parameter to shear includes a known thresholding effect, but does not account for any effects caused by rate of change of fluid shear or cell memory. In principle, these effects could be included in equation (15), but the experiments required to understand their importance have not yet been undertaken. Finally, the calibration methodology presented here has only partially accounted for the effects of bubble absorption and scattering. Again, further measurements are required to better eliminate these biases.
[29] Bioluminescence imaging has the potential to significantly impact a broad range of hydrodynamic research areas, including transient, turbulent, two‐phase flows. Ultimately, it may be possible to use cell bioluminescence to study wave turbulence in the open ocean and surf zone by calibrating the statistical model using bioluminescent species common to coastal red tides. In principle, aerial observations of flow‐induced bioluminescence offer an unprecedented advantage to point measurements and would provide an instantaneous, synoptic view of highly dissipative events over large areas of the ocean surface [Rohr et al., 2002].[/vc_column_text][/vc_tta_section][vc_tta_section title=”References” tab_id=”1550620153638-d3937dba-0633″][vc_column_text]
- Blaser, S., F. Kurisu, H. Satoh, and T. Mino (2002), Hydromechanical stimulation of bioluminescent plankton, Luminescence, 17, 370–380. Wiley Online Library | PubMed | Web of Science | Google Scholar
- Chen, A. K., M. I. Latz, and J. A. Frangos (2003), The use of dinoflagellate bioluminescence to characterize cell stimulation in bioreactors, Biotechnol. Bioeng., 83, 93–103. Wiley Online Library | CAS | PubMed | Web of Science | Google Scholar
- Cox, D. T., K. N. Kobyashi, and A. Okayasu (1996), Bottom shear stress in the surf zone, J. Geophys. Res., 101, 14,337–14,348. Wiley Online Library | ADS | Web of Science | Google Scholar
- Deane, G. B., and M. D. Stokes (1998), Air entrainment processes and bubble size distributions in the surf zone, J. Phys. Oceanogr., 29, 1393–1403. Crossref | ADS | Web of Science | Google Scholar
- Deane, G. B., and M. D. Stokes (2002), Scale dependence of bubble creation mechanisms in breaking waves, Nature, 418, 839–844. Crossref | CAS | ADS | PubMed | Web of Science | Google Scholar
- Farmer, D. M., C. L. McNeil, and B. D. Johnson (1993), Evidence for the importance of bubbles in increasing air‐sea gas flux, Nature, 361, 620–623. Crossref | ADS | Web of Science | Google Scholar
- Garrett, C., M. Li, and D. Farmer (2000), The connection between bubble size spectra and energy dissipation rates in the upper ocean, J. Phys. Oceanogr., 30, 2163–2171. Crossref | ADS | Web of Science | Google Scholar
- Hamman, J. P., and H. H. Seliger (1972), The mechanical triggering of bioluminescence in marine dinoflagellates: Chemical basis, J. Cell Physiol., 80, 397–408. Wiley Online Library | CAS | PubMed | Web of Science | Google Scholar
- Kelly, M. G., and P. Tett (1978), Bioluminescence in the ocean, in Bioluminescence in Action, edited by P. J. Herring, pp. 399–417, Academic, San Diego, Calif. Google Scholar
- Lamarre, E., and W. K. Melville (1991), Air entrainment and dissipation in breaking waves, Nature, 351, 469–472. Crossref | ADS | Web of Science | Google Scholar
- Latz, M. I., and J. Rohr (1999), Luminescent response of the red tide dinoflagellate Lingulodinium polyedrum to laminar and turbulent flow, Limnol. Oceanogr., 44, 1423–1435. Wiley Online Library | Web of Science | Google Scholar
- Latz, M. I., J. F. Case, and R. L. Gran (1994), Excitation of bioluminescence by laminar fluid shear associated with simple Couette flow, Limnol. Oceanogr., 39, 1424–1439. Wiley Online Library | Web of Science | Google Scholar
- Loewen, M. R., and W. K. Melville (1991), Microwave backscatter and acoustic radiation from breaking waves, J. Fluid Mech., 224, 601–623. Crossref | ADS | Web of Science | Google Scholar
- Longuet‐Higgins, M. S. (1974), Breaking waves in deep or shallow water, in Proceedings of the 10th Conference on Naval Hydrodynamics MIT, pp. 597–605, US Gov. Print. Off., Washington, D. C. Google Scholar
- Mann, K. H., and J. R. Lazier (1996), Dynamics of Marine Ecosystems: Biological‐Physical Interactions in the Ocean, Blackwell Sci., Malden, Mass. Google Scholar
- Melville, W. K. (1994), Energy dissipation by breaking waves, J. Phys. Oceanogr., 24, 2041–2049. Crossref | ADS | Web of Science | Google Scholar
- Melville, W. K. (1996), The role of surface‐wave breaking in air‐sea interaction, Annu. Rev. Fluid. Mech., 28, 279–321. Crossref | ADS | Web of Science | Google Scholar
- Morin, J. G. (1983), Coastal bioluminescence: Patterns and functions, Bull. Mar. Sci., 33, 787–817. Web of Science | Google Scholar
- Nauen, J. C. (1998), Biomechanics of two aquatic defense systems, Ph. D. diss., 159 pp., Univ. of Calif., San Diego. Google Scholar
- Rohr, J., J. Allen, J. Losee, and M. I. Latz (1997), The use of bioluminescence as a flow diagnostic, Phys. Lett. A, 228, 408–416. Crossref | CAS | ADS | Web of Science | Google Scholar
- Rohr, J., M. I. Latz, S. Fallon, J. C. Nauen, and E. Hendricks (1998), Experimental approaches towards interpreting dolphin‐stimulated bioluminescence, J. Exp. Biol., 201, 1447–1460. CAS | PubMed | Web of Science | Google Scholar
- Rohr, J., M. Hyman, S. Fallon, and M. I. Latz (2002), Bioluminescence flow visualization in the ocean: An initial strategy based on laboratory experiments, Deep Sea Res., Part I, 49, 2009–2033. Crossref | ADS | Web of Science | Google Scholar
- Seliger, H. H., W. G. Fastie, and W. G. McElroy (1961), Bioluminescence in Chesapeake Bay, Science, 133, 699–700. Crossref | CAS | ADS | PubMed | Web of Science | Google Scholar
- Stokes, M. D., G. B. Deane, S. Vagle, and D. Farmer (2002), Measurements of large bubbles in open‐ocean whitecaps, in Gas Transfer at Water Surfaces, Geophys. Monogr. Ser., vol. 127, edited by M. A. Donelan et al., pp. 278–285. Google Scholar
- Thomas, W. H., and C. H. Gibson (1990), Quantified small‐scale turbulence inhibits a red tide dinoflagellate, Gonyaulax polyedra, Deep Sea Res., Part A, 37, 1583–1593. Crossref | ADS | Web of Science | Google Scholar
- Wallace, D. W. R., and C. D. Wirick (1992), Large air‐sea fluxes associated with breaking waves, Nature, 356, 694–696. Crossref | CAS | ADS | Web of Science | Google Scholar
- Widder, E. A., and J. F. Case (1981), Luminescent microsource activity in bioluminescence of the dinoflagellate, Pyrocystis fusiformis, J. Comput. Phys. A, 145, 517–527. Crossref | Google Scholar
- Widder, E. A., J. F. Case, S. A. Bernstein, S. MacIntyre, M. R. Lowenstine, M. R. Bowlby, and D. P. Cook (1993), A new large volume bioluminescence bathyphotometer with defined turbulence excitation, Deep Sea Res., Part I, 40, 607–627. Crossref | ADS | Web of Science | Google Scholar
(a) Position of intensified camera system and motion-controlled sled exterior to a section of the glass-walled wave flume where wave packets constructively interfere and break (flume is more than 33 m. long). A thin, opaque divider was placed in the flume in order to limit the imaging to a 10 cm. slice of wave.
(b) Example intensified image frame collected during a breaking event. On the right, a subsection of the image is magnified to illustrate individual cell pathways illuminated during flashing and their position within the sample volume (10 cm. thick).
(c) Micrograph of a mature Pyrocystis fusiformis cell illustrating elongated spindle shape and central nucleus. Scale bar is 100 mircometers.[/vc_column_text][/vc_column_inner][/vc_row_inner][vc_row_inner][vc_column_inner][vc_single_image image=”1587″ img_size=”full” alignment=”center”][vc_column_text]Figure 2. Image montage showing (1) an example breaking wave, (b) bioluminescence intensity images, and (c) shear stress calculated from the cell firing model. Intensity images and shear stress images have been averaged over five video frames. The image is approximately 75 cm. across. The wave in the image is moving from left to right, and image sequence starts 0.4 sec. after the initiation of wave breaking (overturn of wave crest). (Top) Regions of high shear stress are associated with the collapse of the overturning wave jet and the turbulent eddy formed in secondary splash-up in front of the wave crest.[/vc_column_text][/vc_column_inner][/vc_row_inner][vc_row_inner][vc_column_inner][vc_single_image image=”3883″ img_size=”full” alignment=”center”][vc_column_text]Figure 3. Images of turbulent energy dissipation inferred from fluid shear stress during wave breaking (as shown in Figure 1). Scale is in log W/kg from about 30 mW/kg to 30 W/kg. The white box in the central plate identifies the cavity crushing and jet interaction region.[/vc_column_text][/vc_column_inner][/vc_row_inner][vc_row_inner][vc_column_inner][vc_single_image image=”2297″ img_size=”full” alignment=”center”][vc_column_text]Figure 4. Two images showing the effects of thresholding to reduce the effects of light scattering from entrained bubbles. (Left) The red regions in the raw image are caused by camera noise and from light scattered by bubbles behind and beside flashing dinoflagellates. (Right) The noise and scattering is removed from the quantitative analysis by image thresholding. Box labeled “A” is located behind the actively breaking wave crest and is discussed in the text. Scale bar is 10 cm.[/vc_column_text][/vc_column_inner][/vc_row_inner][/vc_column][/vc_row][vc_row css=”.vc_custom_1557277275375{padding-right: 25px !important;padding-left: 25px !important;}” el_class=”laptop”][vc_column][vc_custom_heading text=”Figures” font_container=”tag:h3|text_align:left” google_fonts=”font_family:Roboto%3A100%2C100italic%2C300%2C300italic%2Cregular%2Citalic%2C500%2C500italic%2C700%2C700italic%2C900%2C900italic|font_style:500%20bold%20regular%3A500%3Anormal”][vc_row_inner equal_height=”yes” content_placement=”middle” gap=”35″ css=”.vc_custom_1554166982584{margin-top: -25px !important;}”][vc_column_inner width=”1/2″][vc_single_image image=”1573″ img_size=”full” alignment=”center”][/vc_column_inner][vc_column_inner width=”1/2″][vc_column_text]Figure 1. Schematic of experimental setup and orientation of imaged volume relative to the camera.
(a) Position of intensified camera system and motion-controlled sled exterior to a section of the glass-walled wave flume where wave packets constructively interfere and break (flume is more than 33 m. long). A thin, opaque divider was placed in the flume in order to limit the imaging to a 10 cm. slice of wave.
(b) Example intensified image frame collected during a breaking event. On the right, a subsection of the image is magnified to illustrate individual cell pathways illuminated during flashing and their position within the sample volume (10 cm. thick).
(c) Micrograph of a mature Pyrocystis fusiformis cell illustrating elongated spindle shape and central nucleus. Scale bar is 100 mircometers.[/vc_column_text][/vc_column_inner][/vc_row_inner][vc_row_inner equal_height=”yes” content_placement=”middle” gap=”35″][vc_column_inner width=”1/2″][vc_single_image image=”1587″ img_size=”full” alignment=”center”][/vc_column_inner][vc_column_inner width=”1/2″][vc_column_text]Figure 2. Image montage showing (1) an example breaking wave, (b) bioluminescence intensity images, and (c) shear stress calculated from the cell firing model. Intensity images and shear stress images have been averaged over five video frames. The image is approximately 75 cm. across. The wave in the image is moving from left to right, and image sequence starts 0.4 sec. after the initiation of wave breaking (overturn of wave crest). (Top) Regions of high shear stress are associated with the collapse of the overturning wave jet and the turbulent eddy formed in secondary splash-up in front of the wave crest.[/vc_column_text][/vc_column_inner][/vc_row_inner][vc_row_inner equal_height=”yes” content_placement=”middle” gap=”35″][vc_column_inner width=”1/2″][vc_single_image image=”3883″ img_size=”full” alignment=”center”][/vc_column_inner][vc_column_inner width=”1/2″][vc_column_text]Figure 3. Images of turbulent energy dissipation inferred from fluid shear stress during wave breaking (as shown in Figure 1). Scale is in log W/kg from about 30 mW/kg to 30 W/kg. The white box in the central plate identifies the cavity crushing and jet interaction region.[/vc_column_text][/vc_column_inner][/vc_row_inner][vc_row_inner equal_height=”yes” content_placement=”middle” gap=”35″][vc_column_inner width=”1/2″][vc_single_image image=”2297″ img_size=”full” alignment=”center”][/vc_column_inner][vc_column_inner width=”1/2″][vc_column_text]Figure 4. Two images showing the effects of thresholding to reduce the effects of light scattering from entrained bubbles. (Left) The red regions in the raw image are caused by camera noise and from light scattered by bubbles behind and beside flashing dinoflagellates. (Right) The noise and scattering is removed from the quantitative analysis by image thresholding. Box labeled “A” is located behind the actively breaking wave crest and is discussed in the text. Scale bar is 10 cm.[/vc_column_text][/vc_column_inner][/vc_row_inner][/vc_column][/vc_row][vc_row css=”.vc_custom_1556672852388{padding-right: 25px !important;padding-left: 25px !important;}”][vc_column][vc_custom_heading text=”Publications” font_container=”tag:h3|text_align:left” google_fonts=”font_family:Roboto%3A100%2C100italic%2C300%2C300italic%2Cregular%2Citalic%2C500%2C500italic%2C700%2C700italic%2C900%2C900italic|font_style:500%20bold%20regular%3A500%3Anormal”][vc_custom_heading text=”Bioluminescence Imaging of Wave-Induced Turbulence” font_container=”tag:h3|text_align:left” google_fonts=”font_family:Roboto%3A100%2C100italic%2C300%2C300italic%2Cregular%2Citalic%2C500%2C500italic%2C700%2C700italic%2C900%2C900italic|font_style:900%20bold%20regular%3A900%3Anormal”][vc_column_text]
Date Published: Jan 2004
Abstract: The ability to measure turbulent processes on small spatial and temporal scales is a long standing problem in physical oceanography. Here we explore a novel means of measuring fluid shear stress using the cell flashing behavior of bioluminescent dinoflagellates. To illustrate this technique, we present estimates of the heterogeneous, time-varying shear stress inside a breaking wave crest. These results have implications for a better understanding of upper ocean wave physics, air-sea gas transfer, and the biology of planktonic near-surface organisms as well as providing a new quantitative fluid visualization tool.
