Therefore, processes taking place at the termini of marine‐terminating glaciers have a crucial importance and need considerable attention. However, numerical modeling of glacier dynamics is extremely difficult due to a lack of sufficient knowledge of the physical control mechanisms, keeping most models semiempirical [Benn et al., 2007a, 2007b]. Despite significant work directed toward obtaining a realistic estimate of the contribution of melting glaciers to sea level rise, this is still an open issue [Benn et al., 2007a, 2007b; Bassis, 2011; Bassis and Jacobs, 2013; Bassis and Walker, 2013; O’Leary and Christoffersen, 2013]. Difficulties include but are not limited to the occurrence of diverse patterns of events across distinct glaciological regimes and environments. For example, ice breakups in Greenland and Antarctica are rather intermittent and involve large volumes of ice, while ice detachments from tidewater glaciers in other regions, like Svalbard, occur much more frequently and usually constitute a source of much smaller icebergs [Benn et al., 2007a, 2007b]. Both iceberg dimensions and their rates of production depend on glacier dynamics and morphology [Dowdeswell, 1989]. Tidewater glaciers are sensitive to small perturbations in ice flow velocity, water depth, and the temperature at the ice cliff [e.g., Meier and Post, 1987; Vieli et al., 2002], all of which can cause changes in calving intensity. Calving manifests itself with both subaerial and submarine events. Significantly less frequent underwater detachments are often linked with a well‐developed ice foot and are responsible for the production of debris‐rich icebergs surfacing up to 500 m from the ice face; these events are however still poorly understood [Motyka, 1997; Hunter and Powell, 1998]. Numerous and small calving events are difficult to monitor compared to the calving of ice shelves and huge glacier tongues, because of the limited spatial and temporal resolution of generally available satellite images, and because of limitations resulting from the lack of sunlight during polar nights.
New methods are needed to study these dynamic, small‐scale calving processes and quantify their total impact on the ice mass budget. A number of recent studies have used seismic measurements to monitor calving activity. O’Neel et al. [2007] found that most of the energy of calving‐related signals in Alaska is concentrated in a narrow frequency band (1–3 Hz), as later confirmed by combination with time‐lapse photography [Bartholomaus et al., 2012]. Other seismological studies concerning, e.g., detachments of full‐glacier‐thickness icebergs [Walter et al., 2012], application of single‐channel geophone [Köhler et al., 2012], or observation of postcalving seiche effects [Walter et al., 2013], showed the potential of low‐frequency (<50 Hz) monitoring. However, it proved that it is impossible to correlate calved iceberg sizes with signal amplitude; the number of missed events or false detections was often substantial, and submarine events were usually practically invisible in the seismic data.
Technological and methodological advances over the last few years have shown that underwater acoustics can provide a potential solution to these issues. Low‐frequency hydroacoustic signals have been detected by seismic stations and associated with drifting and anchored icebergs in Antarctica [Talandier et al., 2002, 2006]. Higher‐frequency (up to ~44 kHz) measurements of ambient noise made it possible to identify individual subaerial calving events in Alaska and Spitsbergen through spectral and statistical analyses, extending above 1 kHz [Pettit et al., 2012; Tegowski et al., 2012] and suggest possible stages of their evolution [Pettit, 2012]. It was also found that relatively calm conditions in the glacial bays of Svalbard can be as noisy as during moderate sea state with wave heights ranging from 1.25 to 2.5 m, showing significant contribution of melt‐driven cryogenic sounds to the underwater noise field [Tegowski et al., 2011; Deane et al., 2014]. Laboratory measurements of melting samples of glacial ice have in turn revealed higher‐frequency signatures (>1 kHz) [Blondel et al., 2013; Lee et al., 2014], distinct from those of colliding/scraping ice samples [Blondel et al., 2013]. These results motivated further the exploration of the possibilities provided by acoustical detection to monitor dynamic phenomena taking place at the ice‐ocean boundaries. Can unique acoustic features be associated with distinct types of calving events, such as underwater detachments? If so, can these features add to our understanding of the underlying physics and help in autonomous monitoring of calving, one of the main processes leading to the tidewater glaciers’ mass loss?
To address these issues, we conducted continuous high‐frequency acoustic measurements near the terminus of Hans Glacier, a marine‐terminating outlet glacier located in Hornsund fjord, South Spitsbergen, Svalbard, synchronized with high‐resolution time‐lapse photography of the terminal cliff. Hans Glacier covers an area of 53 km2 and has a 1.3 km wide calving face [Vieli et al., 2002]. The glacier is grounded, relatively slow flowing, with a velocity at the front ~150–200 m yr−1 [Blaszczyk et al., 2009] and a front retreat of ~40 m yr−1in the last decade (M. Blaszczyk, personal communication, 2014). It is representative of other tidewater glaciers in Svalbard, with front velocities varying from 0 up to ~260 m yr−1 and average front retreats of ~45 m yr−1 [Blaszczyk et al., 2013]. Here we present the acoustic evolution of different calving styles observed at Hans Glacier, the most frequent being subaerial (here called “typical”), submarine, and subaerial with contact between capsizing iceberg and the ice face. A quantitative analysis of the impact energy of falling ice, estimated from the photographic data, and the acoustic energy below 200 Hz generated by the impact shows a strong correlation between these two variables.[/vc_column_text][/vc_tta_section][vc_tta_section title=”Methods and Data Analysis” tab_id=”1551061276700-75c4d4dd-e2a2″][vc_column_text]
2.1 Acoustic Measurements
The acoustic data were collected on 20, 21, and 24 August 2013 in different locations at the front of the Hans Glacier in Svalbard (Figures S1a and S1b in the supporting information), using an acoustic buoy equipped with a HTI‐96‐MIN omnidirectional hydrophone with sensitivity −165 dB referenced to 1 V/μPa and a flat frequency response between 2 Hz and 30 kHz. Underwater ambient noise was recorded several hundred meters from the ice cliff with 16‐bit dynamic range and 96 kHz sampling. For each deployment, the buoy was lowered just above the sea bottom for a few hours, in line with established good practice [Robinson et al., 2014]. Water depths at the selected locations were, respectively, 10, 45.5, and 13.5 m. To reduce the contribution of noise from breaking waves to the sound field, all measurements were carried out in periods with relatively calm weather conditions.
2.2 Time‐Lapse Photography and Glacier Measurements
The velocity of the crevassed front of Hans Glacier was approximately constant during the entire experiment, as confirmed by field measurements carried out with GPS sensors attached to measuring poles drilled into the ice (Figure S1c in the supporting information). Our 5 megapixel GoPro Hero 3 Silver Edition digital camera took time‐lapse photographs every 0.5 s with 19 mm full‐frame focal length equivalent, f/2.8 aperture, 5.4 × 4.0 mm sensor size and ISO 100 sensitivity. The distance between the nearest part of the glacier wall and the stable rock on which the camera was placed was less than 200 m (see Figure S1b in the supporting information).
2.3 Data Analysis
Sound pressure levels (SPLs) were calculated according to standard practice [Robinson et al., 2014]. We used a 16,384‐point fast Fourier transform and analyzed data in a 0.2 s moving window with 0.25 ms time step to estimate power spectral density. To show differences in SPLs for different frequencies, we used low‐pass and band‐pass zero‐phase Butterworth filters. The limits were chosen to be 100 Hz, 500 Hz, 1 kHz, and 3 kHz to emphasize differences between calving styles. Relative sound pressure levels (ΔSPLs) were calculated by subtracting SPLs of the background noise, not related to calving and recorded shortly before each event, from the total SPLs reported during each detachment. The acoustic energy generated by block‐water impact, Eac,obs, was estimated for 10 subaerial events by low‐pass filtering the noise record at 200 Hz and integrating the mean square pressure over a 6 s interval, chosen to be representative of the duration of impact noise generation, and dividing by ρwc, where ρw is the water density and c is the speed of sound:
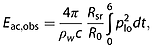(1)where plo is the low‐pass filtered pressure time series, Rsr is the range between the hydrophone and the ice block impact, R0 = 1 m is a reference range, and the factor of 4πaccounts for the surface area of a unit sphere, over which the noise signal must be integrated to obtain total noise energy in joules. The factor Rsr accounts for geometrical spreading and reverberation of the impact noise signal as it propagates from the impact region to the hydrophone and effectively scales the integrated, squared pressure to its value at the reference range R0 from the impact region. Since the propagation range to depth ratio for our observations was ~10 or more, we assumed a cylindrical spreading power law for propagation.Locations of the ice falls were estimated based on time‐lapse photography and panchromatic Landsat 8 satellite imagery taken on 24 August 2013, with a spatial resolution of 15 m. Irregular structure of the ice cliff facilitated this locating procedure and made it possible to mark them on the georeferenced map (see colored dots in Figure S1 in the supporting information). Subsequently, distances from these points to the receiver and to the camera, whose positions were measured with the GPS sensor, were calculated to account for acoustic spreading losses and to obtain glacier heights above the waterline with an accuracy of about ±5 m. Fannytoppen, one of the mountain peaks visible on the photographs, served as a reference point during image processing. The number of pixels in the vertical direction was calculated for both this reference peak and ice wall at each considered location. Taking into account the distances to the objects, it was possible to find the cliff height. Then, heights and lengths of the falling blocks were estimated based on this information. Additionally, heights of the other visible peaks were estimated using the same procedure and compared with real values to test the accuracy of this method. Deviations from the expected values were always less than 5%, despite neglected distortions of the images at their edges.
2.4 Simplified Impact Energy Model
A simple schema is proposed to link generated acoustic emission at the source and energy of the impact between falling blocks and sea surface. The mass of an ice block with dimensions W × H × L is given by M = HLWρ, where ρ is the density of ice, H and L are the height and length of the ice block in its face parallel to the glacier terminus, and W is the block width. The total amount of energy available for the generation of sound resulting from the block‐water interaction is given by
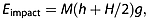(2)where g is the acceleration due to gravity and h is the distance between the bottom of the ice block and the sea surface. Estimates of H and L are available from an analysis of the time‐lapse photographs, but it was not possible to quantify the block width, W, in this way. Instead, motivated by the observation that the block height and length showed a high degree of correlation (0.89, see Table S1 in the supporting information), we assumed that the block width could be expressed as the geometric mean of height and length, multiplied by a constant: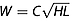 
, where the constant was set to C = 0.15. The numerical value for Cwas chosen based on the casual observation that icebergs in the bay ranged in width from 0.5 to 5 m. Clearly, our estimate of this variable is not particularly well constrained, and the implications of this are raised in the Discussion section. The total energy of the underwater noise radiated by the impact of a falling ice block with the sea surface is assumed to be a constant fraction of its total gravitational potential energy:
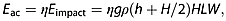(3)where η is a dimensionless constant. The final schema is given by
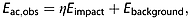(4)where Ebackground is the contribution to the observed noise during the impact interval by noise sources other than the falling ice block, such as freshwater outflow, ice‐wave interactions, and iceberg interactions. There are two unknowns in equation 4, Ebackground and η, and these can be estimated from a least mean squares linear fit between the observed impact noise and the estimates of Eimpact, made from the photographs.
In the uppermost frequency band (1–3 kHz), sound pressure levels remained constant for both typical subaerial and submarine events (Figures 1g and 1i), confirming earlier reports from field studies and laboratory experiments [Tegowski et al., 2011, 2012; Pettit, 2012; Blondel et al., 2013]. Melting blocks of glacial ice, floating on the water surface, generate ambient noise, apparently mostly through the escape of gas bubbles released by melting [Urick, 1971; Tegowski et al., 2011; Blondel et al., 2013; Lee et al., 2014] and iceberg‐wave interactions when surface waves are present [Deane et al., 2014]. Sound intensity increases are most likely when the calved block slides down the ice cliff and interacts with its asperities (Figures 1b, 1e, and 1h), an observation consistent with what can be heard in the recordings (Movie S2 in the supporting information). We conjecture that this type of detachment and its related acoustic signature only occur if the face of the tidewater glacier is not substantially melted below the sea surface (Figures 1b and 1c). Otherwise, the absence of likely contact between the iceberg and the glacier wall precludes any event‐related high‐frequency noise (Figure 1a). In the typical subaerial mode observed for Hans Glacier (Figure 1a and Movie S1 in the supporting information), frequencies below 0.1 kHz show much smaller amplitudes, increasing to levels similar to the 0.1–0.5 kHz band (Figures 1d and 1g) as calving progresses. In the sliding subaerial mode (Figure 1b), lower frequencies still show significant amplitudes (Figures 1e and 1h) as the calved block slides along the irregular surface of the ice cliff. Individual contact events are marked by short, increased SPLs (thin vertical stripes in the spectrograms), corresponding to the short, dynamic interactions with the underwater parts of the glacier wall (Figure 1e). In the submarine calving mode (Figure 1c and Movie S3 in the supporting information), low‐frequency sounds (<0.1 kHz) are more important (Figures 1f and 1i) than in other calving events. They dominate when the calved block reaches the surface at depth‐dependent velocity (determined by its buoyancy) and oscillates before stabilizing; this is generally associated with smaller surface waves after the impact (as can be seen in the Movie S3 in the supporting information). The detailed acoustic signature of this particular mode (Figure 1f) gives more detailed information about what is most likely occurring underwater. First, a few short cracks propagate in the glacier (in this example, at 16 and 20 s in the spectrogram). Then, ice disintegrates, and an ice block separates from the glacier wall and immediately starts floating up (23 to 27 s in this particular example). Finally, this block surfaces (28–35 s) and a secondary impact can be heard (here at 40 s), which most likely depends on how fast the block rose but also on its tilt angle and shape. For all calving modes, the intensity of related underwater noise is still substantial after each event, especially at low frequencies. We interpret this observation as an effect of further disintegrations and collisions between the blocks of glacial ice produced after the main detachment. In many cases, the noise levels are also seen to increase just before the events, which we interpret as signs of precalving glacier activity (e.g., between 10 and 25 s; Figure 1d).
The observations discussed above can be extended to the full set of 12 unambiguously identified calving events. Background noise was subtracted from time‐averaged SPLs, as described earlier (Methods and Data Analysis). The resulting differences (ΔSPL) clearly show that each calving mode stands out by its distinct frequency content, noise level, and spectral slope (Figure 2a). Typical subaerial and submarine events have acoustic signatures below 1 kHz, with systematically distinct peaks (respectively, 35 and 50 Hz). Subaerial events with ice‐ice contacts during the calving similarly show an acoustic signature below 1 kHz, with additional peaks as frequency increases and a second mode at 10 kHz and higher. Spectral slopes below 1 kHz differ for each type of event (17 dB/kHz for typical, 24 dB/kHz for sliding, and 32 dB/kHz for submarine), although their values are most likely to change for other glacier regimes and environmental factors. To help compensate for the influence of different distances from the hydrophone and changing calving size and focus attention on the shape of the spectra, each spectrum was normalized by its maximum amplitude (Figure 2b). The results from this, admittedly small set of observations, tend to support the initial hypothesis that different calving modes can be identified and separated using spectral analysis of underwater ambient noise.
In general, the frequency content of the impact noise from calving events presented here is similar to that reported by Pettit [2012] from Meares Glacier, Alaska. However, Pettit’s conjecture that midfrequency sound (200–600 Hz) generated by iceberg impacting from below would not be as intense as in the case of subaerial events is not supported by our observations. As demonstrated here (Figure 1f), such behavior may occur, possibly due to surface phenomena such as breaking surface waves and splashes generated as a result of large surfacing speeds. Moreover, the study has also revealed high‐frequency ambient noise associated with sliding events, arising most likely as a result of friction between calved iceberg and rough surface of the ice cliff. High‐energy ice‐ice contacts clearly distinguish these kind of events from typical subaerial detachments.
Finally, a simple model was developed to investigate the relationship between generated acoustic energy at the source and the energy of the block‐water impact for subaerial events (see Methods and Data Analysis). High values of correlation coefficients between acoustic emission and both heights and lengths of the calved blocks has motivated this part of the study (Table S1 in the supporting information). Guided by the previous results (Figures 1 and 2), a low‐pass filter with 200 Hz cutoff frequency was applied to the data before further analysis to focus just on impact itself and thereby reduce the influence of highly energetic ice‐ice contacts. Least mean squares analysis, with the application of equation 3, made it possible to link acoustic emission with impact energy (Figure 3). The simple model explains 93% of the variability seen in the data set. Dimensionless energy conversion efficiency ηreaches a value of 5.16 ⋅ 10− 10. For comparison, this coefficient was found to be 4.4 ⋅ 10− 10, when considering acoustic emissions during raindrop‐water impacts, with the assumption that the drop velocity is V = 2 ms− 1 [Guo and Ffowcs Williams, 1991]. This number is somewhat sensitive to the assumptions made about the dimension of icebergs perpendicular to the imaging plane of the camera and therefore impossible to quantify from the images. We believe the value for the energy conversion efficiency determined here is the correct order of magnitude, but a more precise determination awaits later studies.[/vc_column_text][/vc_tta_section][vc_tta_section title=”Concluding Remarks” tab_id=”1551061582991-7d027a21-662c”][vc_column_text]These results confirm that passive acoustics at higher frequencies (up to several tens of kilohertz) can successfully detect individual ice detachments, as already demonstrated by several authors [Tegowski et al., 2011, 2012; Pettit, 2012; Pettit et al., 2012]. This study combined underwater (acoustic) and above‐water (photographic) monitoring of the glacier, also recording several submarine calving events. The results presented here extend the concept of acoustic detection to the identification of distinct calving modes based on the evolution of their spectral characteristics with time. These data shed new light on this poorly understood phenomenon and have led to suggesting a series of physical stages controlling submarine iceberg noise generation.
There are many factors that affect the intensity of underwater noise recorded during ice detachments, including different calving styles and occurrence of “mixed” events, iceberg shapes and sizes, propagation effects, and activity of other sources, e.g., breaking waves, freshwater outflows, or ship traffic. For example, like in this study, friction between calved block and glacier wall may result in greater noise levels that could be expected from visual observations. Similarly, a larger contact zone with the sea surface results in bigger splashes and greater sound intensity underwater. Conversely, these observations fully motivate the distinction between calving styles, which was one of the main goals of this study. As was also demonstrated, the energy of the impact and acoustic emission can be correlated for both sliding and typical subaerial events, knowing the frequency content of underwater noise generated by these types of detachments.
Although the results presented here are limited to 12 well‐constrained calving events from a single tidewater outlet glacier, they demonstrate the potential of conducting studies that simultaneously monitor hydroacoustics and glacial dynamics, in this case through time‐lapse photography. To build on this initial data set, similar experiments should be conducted for longer periods, in different fjords, with calving events of different sizes, in various seasons and environmental conditions. Building on these first observations, they will provide new insight into calving and its role in dynamic interactions at the ice‐ocean boundaries.[/vc_column_text][/vc_tta_section][vc_tta_section title=”References” tab_id=”1551062580506-23316c01-ebcc”][vc_column_text]Amundson, J. M., M. Fahnestock, M. Truffer, J. Brown, M. P. Lüthi, and R. J. Motyka (2010), Ice mélange dynamics and implications for terminus stability, Jakobshavn Isbræ, Greenland, J. Geophys. Res., 115, F01005, doi:10.1029/2009JF001405. Wiley Online Library | ADS | PubMed | Web of Science | Google Scholar
Bartholomaus, T. C., C. F. Larsen, S. O’Neel, and M. E. West (2012), Calving seismicity from iceberg‐sea surface interactions, J. Geophys. Res., 117, F04029, doi:10.1029/2012JF002513. Wiley Online Library | ADS | Web of Science | Google Scholar
Bassis, J. N. (2011), The statistical physics of iceberg calving and the emergence of universal calving laws, J. Glaciol., 57, 3–16, doi:10.3189/002214311795306745. Crossref | ADS | Web of Science | Google Scholar
Bassis, J. N., and S. Jacobs (2013), Diverse calving patterns linked to glacier geometry, Nat. Geosci., 6, 833–836, doi:10.1038/ngeo1887. Crossref | CAS | ADS | Web of Science | Google Scholar
Bassis, J. N., and C. C. Walker (2013), Upper and lower limits on the stability of calving glaciers from the yield strength envelope of ice, Proc. R. Soc. A, 468, 913–931, doi:10.1098/rspa.2011.0422. Crossref | Web of Science | Google Scholar
Benn, D. I., N. R. J. Hulton, and R. H. Mottram (2007a), “Calving laws,” “sliding laws” and the stability of tidewater glaciers, Ann. Glaciol., 46, 123–130, doi:10.3189/172756407782871161. Crossref | ADS | Web of Science | Google Scholar
Benn, D. I., C. R. Warren, and R. H. Mottram (2007b), Calving processes and the dynamics of calving glaciers, Earth Sci. Rev., 82, 143–179, doi:10.1016/j.earscirev.2007.02.002. Crossref | ADS | Web of Science | Google Scholar
Blaszczyk, M., J. A. Jania, and J. O. Hagen (2009), Tidewater glaciers of Svalbard: Recent changes and estimates of calving fluxes, Pol. Polar Res., 30(2), 85–142. Web of Science | Google Scholar
Blaszczyk, M., J. A. Jania, and L. Kolondra (2013), Fluctuations of tidewater glaciers in Hornsund Fjord (Southern Svalbard) since the beginning of the 20th century, Pol. Polar Res., 34(4), 327–352. Web of Science | Google Scholar
Blondel, P., J. Tegowski, and G. B. Deane (2013), Laboratory analyses of transient ice cracking in growlers, in Proceedings of 1st International Conference and Exhibition on Underwater Acoustics, Corfu, Greece, pp. 1253–1260. Google Scholar
Deane, G. B., O. Glowacki, J. Tegowski, M. Moskalik, and P. Blondel (2014), Directionality of the ambient noise field in an Arctic, glacial bay, J. Acoust. Soc. Am., 136(5), EL350, doi:10.1121/1.4897354. Crossref | Web of Science | Google Scholar
Dowdeswell, J. A. (1989), On the nature of Svalbard icebergs, J. Glaciol., 35(120), 224–234. Crossref | Web of Science | Google Scholar
Gardner, A. S., et al. (2013), A reconciled estimate of glacier contributions to sea level rise: 2003–2009, Science, 340, 852–857, doi:10.1126/science.1234532. Crossref | CAS | ADS | PubMed | Web of Science | Google Scholar
Guo, Y. P., and J. E. Ffowcs Williams (1991), A theoretical study on drop impact sound and rain noise, J. Fluid Mech., 227, 345–355, doi:10.1017/S0022112091000149. Crossref | ADS | Web of Science | Google Scholar
Hunter, L. E., and R. D. Powell (1998), Ice foot development at temperate tidewater margins in Alaska, Geophys. Res. Lett., 25(11), 1923–1926, doi:10.1029/98GL01403. Wiley Online Library | ADS | Web of Science | Google Scholar
Jacob, T., J. Wahr, W. T. Pfeffer, and S. Swenson (2012), Recent contributions of glaciers and ice caps to sea level rise, Nature, 482, 514–518, doi:10.1038/nature10847. Crossref | CAS | ADS | PubMed | Web of Science | Google Scholar
Joughin, I., W. Abdalati, and M. Fahnestock (2004), Large fluctuations in speed on Greenland’s Jakobshavn Isbrae Glacier, Nature, 432, 608–610, doi:10.1038/nature03130. Crossref | CAS | ADS | PubMed | Web of Science | Google Scholar
Joughin, I., I. M. Howat, M. Fahnestock, B. Smith, W. Krabill, R. B. Alley, H. Stern, and M. Truffer (2008), Continued evolution of Jakobshavn Isbrae following its rapid speedup, J. Geophys. Res., 113, F04006, doi:10.1029/2008JF001023. Wiley Online Library | ADS | Web of Science | Google Scholar
Kargel, J. S., G. J. Leonard, M. P. Bishop, A. Kääb, and B. H. Raup (Eds.) (2014), Global Land Ice Measurements from Space, Springer Praxis Books, Springer, Berlin. Crossref | Google Scholar
Kaser, G., J. G. Cogley, M. B. Dyurgerov, M. F. Meier, and A. Ohmura (2006), Mass balance of glaciers and ice caps: Consensus estimates for 1961–2004, Geophys. Res. Lett., 33, L19501, doi:10.1029/2006GL027511. Wiley Online Library | ADS | PubMed | Web of Science | Google Scholar
Köhler, A., A. Chapuis, C. Nuth, J. Kohler, and C. Weidle (2012), Autonomous detection of calving‐related seismicity at Kronebreen, Svalbard, Cryosphere, 6, 393–406, doi:10.5194/tc-6-393-2012. Crossref | ADS | Web of Science | Google Scholar
Lee, K. M., P. S. Wilson, and E. C. Pettit (2014), Underwater sound radiated by bubbles released by melting glacier ice, in Proceedings of Meetings on Acoustics, vol. 20, 070004, doi:10.1121/1.4866768. Google Scholar
Meier, M. F., and A. Post (1987), Fast tidewater glaciers, J. Geophys. Res., 92(B9), 9051–9058, doi:10.1029/JB092iB09p09051. Wiley Online Library | ADS | Web of Science | Google Scholar
Meier, M. F., M. B. Dyurgerov, U. K. Rick, S. O’Neel, W. T. Pfeffer, R. S. Anderson, S. P. Anderson, and A. F. Glazovsky (2007), Glaciers dominate eustatic sea‐level rise in the 21st century, Science, 317, 1064–1067, doi:10.1126/science.1143906. Crossref | CAS | ADS | PubMed | Web of Science | Google Scholar
Motyka, R. J. (1997), Deep‐water calving at LeConte Glacier, southeast Alaska, in Calving Glaciers: Report of a Workshop, February 28–March 2, 1997, BPRC Rep., vol. 15, edited by C. J. Van der Veen, pp. 115–118, Byrd Polar Res. Cent., Ohio State Univ., Columbus. Google Scholar
Motyka, R. J., L. Hunter, K. A. Echelmeyer, and C. Connor (2003), Submarine melting at the terminus of a temperate tidewater glacier, LeConte Glacier, Alaska, USA, Ann. Glaciol., 36, 57–65, doi:10.3189/172756403781816374. Crossref | ADS | Web of Science | Google Scholar
O’Leary, M., and P. Christoffersen (2013), Calving on tidewater glaciers amplified by submarine frontal melting, Cryosphere, 7, 119–128, doi:10.5194/tc-7-119-2013. Crossref | ADS | Web of Science | Google Scholar
O’Neel, S., H. P. Marshall, D. E. McNamara, and W. T. Pfeffer (2007), Seismic detection and analysis of icequakes at Columbia Glacier, Alaska, J. Geophys. Res., 112, F03S23, doi:10.1029/2006JF000595. Wiley Online Library | ADS | Web of Science | Google Scholar
Pettit, E. C. (2012), Passive underwater acoustic evolution of a calving event, Ann. Glaciol., 53, 113–122, doi:10.3189/2012AoG60A137. Crossref | ADS | Web of Science | Google Scholar
Pettit, E. C., J. A. Nystuen, and S. O’Neel (2012), Listening to glaciers: Passive hydroacoustics near marine‐terminating glaciers, Oceanography, 25, 104–105, doi:10.5670/oceanog.2012.81. Crossref | Web of Science | Google Scholar
Pfeffer, W. T., J. T. Harper, and S. O’Neel (2008), Kinematic constraints on glacier contributions to 21st‐century sea‐level rise, Science, 321, 1340–1343, doi:10.1126/science.1159099. Crossref | CAS | ADS | PubMed | Web of Science | Google Scholar
Rignot, E., G. Casassa, P. Gogineni, W. Krabill, A. Rivera, and R. Thomas (2004), Accelerated ice discharge from the Antarctic Peninsula following the collapse of Larsen B ice shelf, Geophys. Res. Lett., 31, L18401, doi:10.1029/2004GL020697. Wiley Online Library | CAS | ADS | Web of Science | Google Scholar
Rignot, E., I. Velicogna, M. R. van den Broeke, A. Monaghan, and J. T. M. Lenaerts (2011), Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise, Geophys. Res. Lett., 38, L05503, doi:10.1029/2011GL046583. Wiley Online Library | ADS | Web of Science | Google Scholar
Robinson, S. P., P. A. Lepper, and R. A. Hazelwood (2014), Good practice guide for underwater noise measurement, National Measurement Office, Marine Scotland, The Crown Estate, NPL Good Practice Guide No. 133, ISSN: 1368–6550. Google Scholar
Scambos, T., C. Hulbe, and M. Fahnestock (2003), Climate‐induced ice shelf disintegration in the Antarctic Peninsula, Antarct. Res. Ser., 79, 79–92, doi:10.1029/AR079p0079. Wiley Online Library | Web of Science | Google Scholar
Scambos, T. A., J. A. Bohlander, C. A. Shuman, and P. Skvarca (2004), Glacier acceleration and thinning after ice shelf collapse in the Larsen B embayment, Antarctica, Geophys. Res. Lett., 31, L18402, doi:10.1029/2004GL020670. Wiley Online Library | CAS | ADS | Web of Science | Google Scholar
Straneo, F., R. G. Curry, D. A. Sutherland, G. S. Hamilton, C. Cenedese, K. Våge, and L. A. Stearns (2011), Impact of fjord dynamics and glacial runoff on the circulation near Helheim Glacier, Nat. Geosci., 4, 322–327, doi:10.1038/ngeo1109. Crossref | CAS | ADS | Web of Science | Google Scholar
Talandier, J., O. Hyvernaud, E. A. Okal, and P.‐F. Piserchia (2002), Long‐ range detection of hydroacoustic signals from large icebergs in the Ross Sea, Antarctica, Earth Planet. Sci. Lett., 203(1), 519–534, doi:10.1016/S0012-821X(02)00867-1. Crossref | CAS | ADS | Web of Science | Google Scholar
Talandier, J., O. Hyvernaud, D. Reymond, and E. A. Okal (2006), Hydroacoustic signals generated by parked and drifting icebergs in the Southern Indian and Pacific Oceans, Geophys. J. Int., 165, 817–834, doi:10.1111/j.1365-246X.2006.02911.x. Wiley Online Library | ADS | Web of Science | Google Scholar
Tegowski, J., G. B. Deane, A. Lisimenka, and P. Blondel (2011), Detecting and analyzing underwater ambient noise of glaciers on Svalbard as indicator of dynamic processes in the Arctic, in Proceedings of the 4th UAM Conference, Kos, Greece, pp. 1149–1154. Google Scholar
Tegowski, J., G. B. Deane, A. Lisimenka, and P. Blondel (2012), Spectral and statistical analyses of ambient noise in Spitsbergen Fjords and identification of glacier calving events, in Proceedings of the 11th European Conference on Underwater Acoustics, Edinburgh, Scotland, pp. 1667–1672. Google Scholar
Urick, R. J. (1971), The noise of melting icebergs, J. Acoust. Soc. Am., 50, 337, doi:10.1121/1.1912637. Crossref | ADS | Web of Science | Google Scholar
Vieli, A., J. A. Jania, and L. Kolondra (2002), The retreat of a tidewater glacier: Observations and model calculations on Hansbreen, Spitsbergen, J. Glaciol., 48(163), 592–600, doi:10.3189/172756502781831089. Crossref | ADS | Web of Science | Google Scholar
Walter, F., J. M. Amundson, S. O’Neel, M. Truffer, M. Fahnestock, and H. A. Fricker (2012), Analysis of low‐frequency seismic signals generated during a multiple‐iceberg calving event at Jakobshavn Isbræ, Greenland, J. Geophys. Res., 117, F01036, doi:10.1029/2011JF002132. Wiley Online Library | CAS | ADS | Web of Science | Google Scholar
Walter, F., M. Olivieri, and J. F. Clinton (2013), Calving event detection by observation of seiche effects on the Greenland fjords, J. Glaciol., 59(213), 162–178, doi:10.3189/2013JoG12J118. Crossref | ADS | Web of Science | Google Scholar[/vc_column_text][/vc_tta_section][/vc_tta_accordion][/vc_column][/vc_row][vc_row css=”.vc_custom_1557277936215{padding-right: 25px !important;padding-left: 25px !important;}” el_class=”laptop”][vc_column][vc_custom_heading text=”Figures” font_container=”tag:h3|text_align:left” google_fonts=”font_family:Roboto%3A100%2C100italic%2C300%2C300italic%2Cregular%2Citalic%2C500%2C500italic%2C700%2C700italic%2C900%2C900italic|font_style:500%20bold%20regular%3A500%3Anormal”][vc_row_inner equal_height=”yes” content_placement=”middle” gap=”35″ css=”.vc_custom_1554236695404{margin-top: -25px !important;}”][vc_column_inner width=”1/2″][vc_single_image image=”3947″ img_size=”full” alignment=”center”][/vc_column_inner][vc_column_inner width=”1/2″][vc_column_text]Figure 1. Sketches of calving modes for (a–c) three representative events together with (d–f) ambient noise spectrograms and frequency‐averaged SPLs calculated after the application of (g–i) low‐pass (black, blue, and red) and band‐pass (green) zero‐phase Butterworth filters. Starting times of the recordings are, respectively, 12:29:48 UTC for 24 August, 15:27:22 UTC for 20 August, and 17:48:25 UTC for 21 August.[/vc_column_text][/vc_column_inner][/vc_row_inner][vc_row_inner equal_height=”yes” content_placement=”middle” gap=”35″][vc_column_inner width=”1/2″][vc_single_image image=”3948″ img_size=”full” alignment=”center”][/vc_column_inner][vc_column_inner width=”1/2″][vc_column_text]Figure 2. Time‐averaged sound pressure levels (SPLs), both (a) before and (b) after normalization by their maximum values, during the 12 selected calving events, smoothed and with no significant background noise. For typical subaerial detachments, event‐averaged nonnormalized ΔSPL is shown with ±2 standard deviations (the smaller number of events in the other modes precluded the use of standard deviations).[/vc_column_text][/vc_column_inner][/vc_row_inner][vc_row_inner equal_height=”yes” content_placement=”middle” gap=”35″][vc_column_inner width=”1/2″][vc_single_image image=”3949″ img_size=”full” alignment=”center”][/vc_column_inner][vc_column_inner width=”1/2″][vc_column_text]Figure 3. Relationship between the energy of block‐water impact and both observed and predicted acoustic emissions. The coefficient of determination reached a value of 0.93. A low‐pass Butterworth zero‐phase filter with 200 Hz cutoff frequency was applied to the data before this analysis.[/vc_column_text][/vc_column_inner][/vc_row_inner][/vc_column][/vc_row][vc_row css=”.vc_custom_1557278002414{padding-right: 25px !important;padding-left: 25px !important;}” el_class=”phone”][vc_column][vc_custom_heading text=”Figures” font_container=”tag:h3|text_align:left” google_fonts=”font_family:Roboto%3A100%2C100italic%2C300%2C300italic%2Cregular%2Citalic%2C500%2C500italic%2C700%2C700italic%2C900%2C900italic|font_style:500%20bold%20regular%3A500%3Anormal”][vc_row_inner equal_height=”yes” content_placement=”middle” gap=”35″ css=”.vc_custom_1554236695404{margin-top: -25px !important;}”][vc_column_inner][vc_single_image image=”3947″ img_size=”full” alignment=”center”][vc_column_text]Figure 1. Sketches of calving modes for (a–c) three representative events together with (d–f) ambient noise spectrograms and frequency‐averaged SPLs calculated after the application of (g–i) low‐pass (black, blue, and red) and band‐pass (green) zero‐phase Butterworth filters. Starting times of the recordings are, respectively, 12:29:48 UTC for 24 August, 15:27:22 UTC for 20 August, and 17:48:25 UTC for 21 August.[/vc_column_text][/vc_column_inner][/vc_row_inner][vc_row_inner equal_height=”yes” content_placement=”middle” gap=”35″][vc_column_inner][vc_single_image image=”3948″ img_size=”full” alignment=”center”][vc_column_text]Figure 2. Time‐averaged sound pressure levels (SPLs), both (a) before and (b) after normalization by their maximum values, during the 12 selected calving events, smoothed and with no significant background noise. For typical subaerial detachments, event‐averaged nonnormalized ΔSPL is shown with ±2 standard deviations (the smaller number of events in the other modes precluded the use of standard deviations).[/vc_column_text][/vc_column_inner][/vc_row_inner][vc_row_inner equal_height=”yes” content_placement=”middle” gap=”35″][vc_column_inner][vc_single_image image=”3949″ img_size=”full” alignment=”center”][vc_column_text]Figure 3. Relationship between the energy of block‐water impact and both observed and predicted acoustic emissions. The coefficient of determination reached a value of 0.93. A low‐pass Butterworth zero‐phase filter with 200 Hz cutoff frequency was applied to the data before this analysis.[/vc_column_text][/vc_column_inner][/vc_row_inner][/vc_column][/vc_row][vc_row css=”.vc_custom_1556674361661{padding-right: 25px !important;padding-left: 25px !important;}”][vc_column][vc_custom_heading text=”Publications” font_container=”tag:h3|text_align:left” google_fonts=”font_family:Roboto%3A100%2C100italic%2C300%2C300italic%2Cregular%2Citalic%2C500%2C500italic%2C700%2C700italic%2C900%2C900italic|font_style:500%20bold%20regular%3A500%3Anormal”][vc_custom_heading text=”Underwater acoustic signatures of glacier calving” font_container=”tag:h3|text_align:left” google_fonts=”font_family:Roboto%3A100%2C100italic%2C300%2C300italic%2Cregular%2Citalic%2C500%2C500italic%2C700%2C700italic%2C900%2C900italic|font_style:900%20bold%20regular%3A900%3Anormal”][vc_column_text]Glowacki, O, Deane GB, Moskalik M, Blondel P, Tegowski J, Blaszczyk M. 2015. Underwater acoustic signatures of glacier calving. Geophysical Research Letters. :2014GL062859.
Date Published: Feb 2015
Abstract: Climate-driven ice-water interactions in the contact zone between marine-terminating glaciers and the ocean surface show a dynamic and complex nature. Tidewater glaciers lose volume through the poorly understood process of calving. A detailed description of the mechanisms controlling the course of calving is essential for the reliable estimation and prediction of mass loss from glaciers. Here we present the potential of hydroacoustic methods to investigate different modes of ice detachments. High-frequency underwater ambient noise recordings are combined with synchronized, high-resolution, time-lapse photography of the Hans Glacier cliff in Hornsund Fjord, Spitsbergen, to identify three types of calving events: typical subaerial, sliding subaerial, and submarine. A quantitative analysis of the data reveals a robust correlation between ice impact energy and acoustic emission at frequencies below 200 Hz for subaerial calving. We suggest that relatively inexpensive acoustic methods can be successfully used to provide quantitative descriptions of the various calving types.
We would like to give thanks to:
[/vc_column_text][vc_row_inner][vc_column_inner width=”1/2″ offset=”vc_col-xs-6″][vc_single_image image=”3940″ img_size=”large” alignment=”center” onclick=”custom_link” img_link_target=”_blank” link=”https://ncn.gov.pl/?language=en”][/vc_column_inner][vc_column_inner width=”1/2″ offset=”vc_col-xs-6″][vc_single_image image=”3943″ img_size=”medium” alignment=”center” onclick=”custom_link” img_link_target=”_blank” link=”https://www.forskningsradet.no/en/Home_page/1177315753906″][/vc_column_inner][/vc_row_inner][vc_row_inner][vc_column_inner width=”1/2″ offset=”vc_col-xs-6″][vc_single_image image=”3944″ img_size=”medium” alignment=”center” onclick=”custom_link” img_link_target=”_blank” link=”https://www.igf.edu.pl/home.php”][/vc_column_inner][vc_column_inner width=”1/2″ offset=”vc_col-xs-6″][vc_single_image image=”3869″ img_size=”medium” alignment=”center” onclick=”custom_link” img_link_target=”_blank” link=”https://www.onr.navy.mil/”][/vc_column_inner][/vc_row_inner][/vc_column][/vc_row][vc_row css=”.vc_custom_1556674428318{padding-right: 10px !important;padding-left: 10px !important;}”][vc_column][vc_btn title=”^ Top” style=”flat” size=”xs” align=”right” link=”url:%23top|||”][/vc_column][/vc_row][/vc_section]